Example Problems

Small-Angle Scattering

Two perfectly spherical latex particles of diameter d=10 nm form a rigid dimer. The two spheres touch, i.e., their centers are separated by a = 10 nm. The dimers are investigated by solution scattering.

1. Compute and plot the scattered intensity I(q), q=pi s, for a single d=10 nm latex particle using the Guinier approximation.
2. Use the parallel axis theorem to compute I(q) for the dimer. Plot I(q) versus q.

How would the pattern change if the distance between the centers of the spheres were increased?

How would the pattern change if the diameter d for each latex sphere were decreased for constant a?

Small Angle Scattering from rodlike molecules gives the following intensity distribution

Determine the radius of gyration for the scatterer’s cross section.

Qualitatively, sketch the shape of the Guinier plot one would obtain if the particle were spherical. Comment on the contribution from the rods length and their cross-section to this graph.

Citrus Tristeza virus, a rod-like RNA-plant virus, is investigated by neutron solution scattering. In 50% D2O, the coherent contribution to the scattered intensity, I(q) with q=2 pi s, is measured as in Table 1. The corresponding values for the experiment performed in 37% D2O are listed in Table 2.

Table 1.

Table 2

1. Describe the technique of contrast matching in neutron scattering.
2. State what information you can extract from the above data and what methods of analysis you can employ.
3. Analyze the data with a Gunier type plot and state your results. What additional measurements do you need to come to firm conclusions?

Three different types of Guinier plots are used to determine some important dimensions of differently shaped molecules from small-angle scattering.
a. List the categories of molecules that can be investigated in terms of their shape.
b. Explain the nature of the methods employed.
c. Determine the molecule’s radius of gyration and its maximum dimension from the following data for myoglobin.\

To determine the maximum dimension, assume that the particle is homogeneous and it has a simple geometric shape.

Cryo-electron microscopy

1. Give an outline of the basic operating principles of the scanning electron microscope.
2. Describe some of the ways in which high-energy electrons interact with matter and how they are exploited in the scanning electron microscope to yield various types of information about a specimen.

1. Estimate the theoretical resolving power of a transmission electron microscope (TEM) operating at 100 kV, if the numerical aperture of the objective lens is 0.01.
2. Explain how aberrations in a TEM influence the resolution actually achieved.
3. If the objective lens of a TEM has a coefficient of spherical aberration of 3 mm, and there are no other aberrations, what is the optimum effective numerical aperture for 100 kV electrons?
4. What two other factors may make it desirable to limit the objective aperture?

Give an account of the way in which spherical aberration can affect the resolving power of the objective lens of an electron microscope.

Suggest how theseeffects can be minimized and what criteria might finally limit such partial remedies.

A specimen containing a point-to-point spacing of 0.27 nm is introduced into an electron microscopeobjective of numerical aperture 0.01. When operating with an accelerating voltage of 100 kV show that theoretically it should be possible to resolve a spacing of the given magnitude.

If the objectivelens has a coefficient of spherical aberration of 2 nm, how will your argument and conclusion have to be modified?

Compare and contrast the physical principles that determine the resolution of the scanning electron microscope with those of the transmission instrument.

Indicate how the resolution of the transmission instrument might be further affected by lens aberrations.

Crystallography

(a) Explain the meaning of the following crystallographic terms:

1. Unit cell
2. Asymmetric unit
3. Bravis lattice
4. Screw axis
5. Gluide plane

(b) Draw a diagram for space group P21/c with the origin at the intersection of the 21 screw axis, and with the c-glide plane. Clearly make all the symmetry elements on the diagram.

Redraw the space group diagram, placing the origin on the center of symmetry and label the symmetry elements. Write down the coordinates of the general equivalent positions. What special positions occur in this space group? What are the independent conditions limiting X-ray reflection for P2₁/c?

A crystal of the oxygen-binding protein haemoglobin was mounted on a precession camera with a crystal to film distance of 60 mm and a CuKɑ X-ray source with a wavelength of 1.5418 Å. Precession photographs of the a*b* and a*c* nets were recorded. On the photographs containing the hk0 reflections, the distances between the pairs of diffraction spots were: -18,0,0 and 18,0,0 = 34.76 mm; 0,-20,0 and 0,20,0 = 37.84 mm.

The distance between the 0,0,-12 and 0,0,12 was 33.90 mm on the h0l photographs. Assuming the crystal was orthorhombic, determine the unit cell parameters, a,b, and c, and the unit cell volume in A³.

The haemoglobin crystals contain four asymmetric units per unit cell, with one haemoglobin molecule per asymmetric unit, and have a density of 1.2 gcm^-3

Write a detailed account of one of the following topics:

• The molecular replacement method for crystal structure determination.
• Dynamic resolved crystallography using X-ray Free Electron Laser sources.
• X-ray structure determination by MAD methods at a synchrotron.
• Micro-electron diffraction.

Explain the meaning of the following crystallographic terms

1. Space group
2. screw axis
3. gluide plane
4. systematic absences

For each of the space groups: P21/C, Cm, Ibca:

1. Write down the parent point group and crystal system.
2. List the full meaning conveyed by the symbol
3. State the independent conditions limiting X-ray reflection

Draw diagrams to show a set of general positions and the corresponding set of symmetry elements for space group Cm, and give the coordinates of the general equivalent positions.

Give a brief account of the oscillation, and historical Weissenberg and precession methods of X-ray data collection. Comment on the advantages and disadvantages of each method.

A substance crystallizes in space group Pnma with four molecules per unit cell. Precession photographs of a crystal mounted about its c axis were taken on a camera with a crystal-to-film distance of 60.0 mm, using CuKɑ radiation of wavelength 1.5418Å. On the h0l photograph, the distances between the pairs of diffraction spots 200, -200 and 004, 00-4 were 68.27 mm and 99.47 mm, respectively. If the distance between the axial reflections 020 and 0-20 on the okl photograph was 92.97 mm, calculate the values of the unit cell parameters a, b, and c, and the volume of the unit cell, V, in ų.

Determine the molecular weight, Mr, of the substance is the crystal density is 8.965 g cm^-3 and N_Avog is 0.60221.

Write short notes on the following topics:

1. The atomic scattering factor
2. The structure factor
3. Thermal vibrations of atoms in solids
4. The phase problem in structure analysis

A compound containing platinum (Pt) and some lighter atoms, crystallizes with four Pt atoms in the unit cell with the following atomic positions

1. (0.00, 0.10, 0.25)
2. (0.00, 0.90, 0.75)
3. (0.00, 0.60, 0.75)
4. (0.00, 0.40, 0.25)

If the experimentally observed structure factors Fo(111) and Fo(333) are 191 and 281, respectively, calculate the percentage contribution to the structure factors due to the Pt atoms only, relative to the values observed for all atoms in the unit cell.  The values of the atomic scattering factors f_Pt(111) and f_Pt(333) are 73.5 and 59.5, respectively.

Explain the meaning of the terms:

1. Screw axis
2. Glide plane
3. Limiting conditions
4. Space group

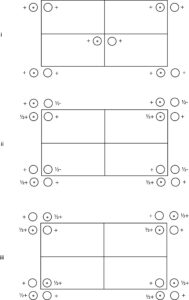
The space group diagrams illustrated below show a set of general equivalent positions in a unit cell. For each case:

1. Draw diagrams showing the corresponding set of symmetry elements.
2. List the coordinates of the general equivalent positions.
3. State the independent conditions limiting X-ray reflection.
4. Write down the parent point group nd crystal system.

Outline with the aid of a suitable sketch, the concept of the reciprocal lattice in X-ray crytallography.

Derive the Laue equations which define the direction of scattering of X-rays by crystalline solids.

USi crystallizes in the orthorhombic system with a=5.65, b=7.65, and c=3.90 Å and z=4. The U atoms lie at positions

1. (0.125, 0.200, 0.250)
2. (-0.125, -0.200, -0.250)
3. (0.375, 0.700, 0.250)
4. (-0.375, -0.700, -0.250)

Calculate the structure factors (a) F(200) and (b) F(111). The contributions to the structure factors from Si may be neglected. The atomic scattering factors for U are tabulated below as a function of (sin θ)/ƛ.

Multiple techniques